Errata

In the paper Fusing filters with integer linear programming, we convert combinator programs to linear programs to find the best fusion clustering. It may seem reasonable to only allow fusion between combinators of the same size, but the problem is filters have an unknown output size.

Instead, we restrict fusion so that two combinators of different sizes may only be fused together if they have some ancestor nodes of the same size, and all four are fused together. We define a function parents to classify these ancestor nodes of the same size, but the paper definition of parents is incorrect and in some cases returns multiple ancestors. If there are multiple ancestor nodes of the same size, choosing the wrong ones may unnecessarily prohibit fusion.

Below, I will show an example of how parents is used, an example where the paper definition can give poor fusion, and finally a fixed definition of parents.

Simple example

Let us first look at how a simple function is fused.

fun xs
 = let as  = filter (>0) xs
       bs  = filter (<0) xs
       cs  = map    (+1) as
       ds  = map    (-1) bs
   in (cs, ds)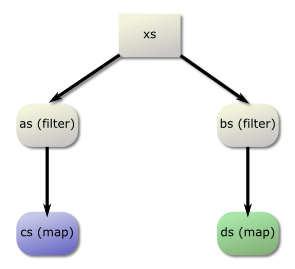

Graph of fun

Notice that cs and ds have different loop sizes, and so are coloured differently in the graph. Both as and bs have the same size and can be fused together; as can be fused into cs and bs can be fused into ds. However, cs and ds can only be fused together if as and bs are in the same group.

In this case, parents cs ds = [(as,bs)], meaning that cs and ds may only be fused together if as, bs, cs and ds are all fused together.

Multiple parents

In the case of a vertical line of filters, a pair of nodes may have multiple ancestors with the same size. Choosing the correct ancestors is particularly important when there are fusion-preventing edges.

filts ms
 = let ns  = filter (>0)    ms

       sum = fold   (+) 0   ns
       ls  = filter (>sum)  ns
       rs  = filter odd     ns

       ls' = map    (+1)    ls
       rs' = map    (-1)    rs
   in  (ls', rs')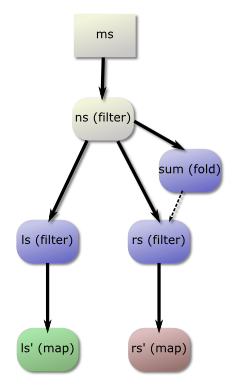

Graph of filts

Here, the question is whether ls' and rs' can be fused together. There are multiple ancestors with the same type: (ls,rs) and (ns,ns). Choosing (ns,ns) will actually disallow ls' and rs' from being fused together, because of the fusion-preventing path between ns and rs'. On the other hand, choosing (ls,rs) allows fusion. In this case, (ls,rs) is the correct choice.

Solution

One simple solution is to modify parents to choose the “closest” ancestors when there are multiple. Given the original definition:

parents a b
 | size a == size b
 =  [ (a, b) ]
 | otherwise
 =  [ parents a' b  | a' <- trans a ]
 ++ [ parents a  b' | b' <- trans b ]

This can be modified to keep track of distance, and return the minimum ancestor:

parents a b
 = map fst
 $ parents' a b 0


parents' a b dist
 | size a == size b
 =  [ ((a, b), dist) ]

 | otherwise
 = sortBy (compare `on` snd)
 $  [ parents a' b  (dist+1) | a' <- trans a ]
 ++ [ parents a  b' (dist+1) | b' <- trans b ]